[Machine Learning] chapter5 - 트리 알고리즘

1. 결정트리

로지스틱 회귀로 와인 분류하기

import pandas as pd
wine = pd.read_csv('https://bit.ly/wine_csv_data')

wine.head()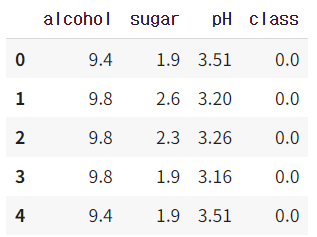

 

- 처음 3개의 열(alcohol, sugar, pH)은 알코올 도수, 당도, pH 값을 나타낸다.

- 네 번째 열 (class)은 타깃값으로 0이면 레드 와인, 1이면 화이트 와인이다.

- 화이트 와인이 양성 클래스이고 레드 와인과 화이트 와인을 구분하는 이진 분류 문제이다.

 

wine.describe()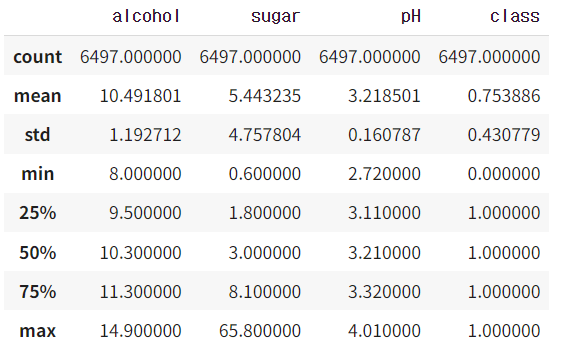

- 위 그림에서 알 수 있는 것은 도수, 당도, pH 값의 스케일이 다르다는 것이다.

 

data = wine[['alcohol','sugar','pH']].to_numpy()
target = wine['class'].to_numpy()

from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(data, target, test_size=0.2, random_state=42)

from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)

from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_scaled, train_target)
print(lr.score(train_scored, train_target))
print(lr.score(test_scaled, test_target))
>>> 0.7808350971714451
>>> 0.7776923076923077

print(lr.coef_, lr.intercept_)
>>> [[ 0.51268071  1.67335441 -0.68775646]] [1.81773456]

 

결정트리

- 결정 트리 (Decision Tree) 모델은 분류(Classification)와 회귀(Regression)를 위한 비모수적 지도 학습 방법이다.

- 데이터의 특징(feature)으로부터 유추된 단순한 if-then-else 규칙을 통해서 목표 변수를 예측한다.

- 데이터를 잘 나눌 수 있는 질문을 찾는다면 분류 정확도를 높일 수 있다.

- 트리는 구간별 상수 함수이고, 트리의 깊이가 깊을 수록 복잡하고 정밀한 예측이 가능하다.

from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(random_state=42)
dt.fit(train_scaled, train_target)
print(dt.score(train_scaled, train_target))
print(dt.score(test_scaled, test_target))
>>> 0.996921300750433
>>> 0.8592307692307692

import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
plt.figure(figsize=(10,7))
plot_tree(dt)
plt.show()

 

- 루트 노드(Root Node)는 트리의 맨 위에 위치한 첫 번째 노드이다.

- 전체 데이터에서 가장 중요한 기준(feature)을 사용하여 처음 분할을 수행한다.

 

- 내부 노드(Internal Node / Decision Node)는 데이터를 특정 기준(feature, 임계값)에 따라 둘 이상으로 나누는 노드이다.

- 각각의 내부 노드는 조건문(if-then)을 포함하고 있다.

 

- 잎 노드 (Leaf Node / Terminal Node)는 더 이상 분할되지 않는 최종 노드로 실제 예측값이다.

- 분류 문제에서는 클래스 라벨, 회귀 문제에서는 평균값이 주어진다.

 

- 위 그림은 너무 복잡하니 트리의 깊이를 제한해서 출력한다.

- 또한 클래스에 맞게 노드의 색을 칠해 어떤 특성으로 노드가 나뉘어지는게 확인할 수 있다.

plt.figure(figsize=(10,7))
plot_tree(dt, max_depth=1, filled=True, feature_names=['alcohol','sugar','pH'])
plt.show()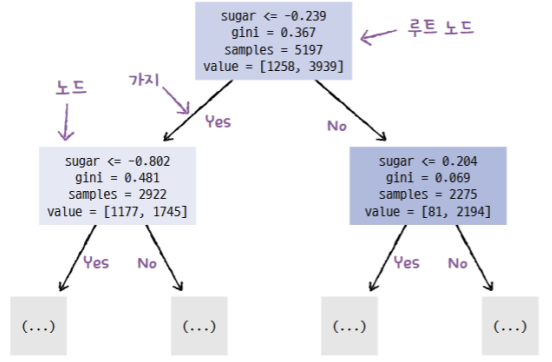

 

불순도

- gini는 지니 불순도를 의미한다.

- DecisionTreeClassifier 클래스의 criterion 매개변수 기본값이 'gini'이다.

- criterion 매개변수는 노드에서 데이터를 분할할 기준을 정하는 것이다.

- 지니 불순도  = 1 - (음성 클래스 비율^2 + 양성 클래스 비율^2)

- 위 트리 그림에서 지니 불순도는 1 - ((1258/5197)^2 + (3939/5179)^2) = 0.367

 

- 결정 트리 모델은 부모 노드와 자식 노드의 불순도 차이가 가능한 크도록 트리를 성장 시킨다.

 

- 부모 노드의 불순도와 자식 노드의 불순도의 차를 정보 이득(information gain)이라고 한다.

- 모든 요소가 하나의 클래스에 속할 때 Gini 값은 0이다. -> 순수 노드

- Gini 값이 높을수록 클래스가 섞여있는 것이다.

- 일반적으로 CART (Classification and Regression Tree)에서 사용된다.

- 엔트로피에 비해 로그 연산이 없기 때문에 계산이 빠르다.

 

- DecisionTreeClassifier 클래스에서 criterion = 'entropy'를 지정해서 엔트로피 불순도를 사용할 수 있다.

- 지니 불순도처럼 제곱이 아니라 밑이 2인 로그를 사용하여 곱한다.

- 순수 노드일 경우 엔트로피는 0이다.

- 엔트로피가 높을수록 클래스가 섞여있는 것이다.

- ID3, C4.5, C5.0과 같은 알고리즘에서 사용된다.

 

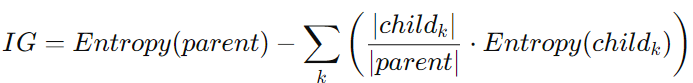
가지치기

- 결정 트리에서 가지치기를 하는 가장 간단한 방법은 자라날 수 있는 트리의 최대 깊이를 지정한다.

dt = DecisionTreeClassifier(max_depth=3, random_state=42)
dt.fit(train_scaled, train_target)
print(dt.score(train_scaled, train_target))
print(dt.score(test_scaled, test_target))
>>> 0.8454877814123533
>>> 0.8415384615384616

plt.figure(figsize=(20,15))
plot_tree(dt, filled=True, feature_names=['alcohol','sugar','pH'])
plt.show()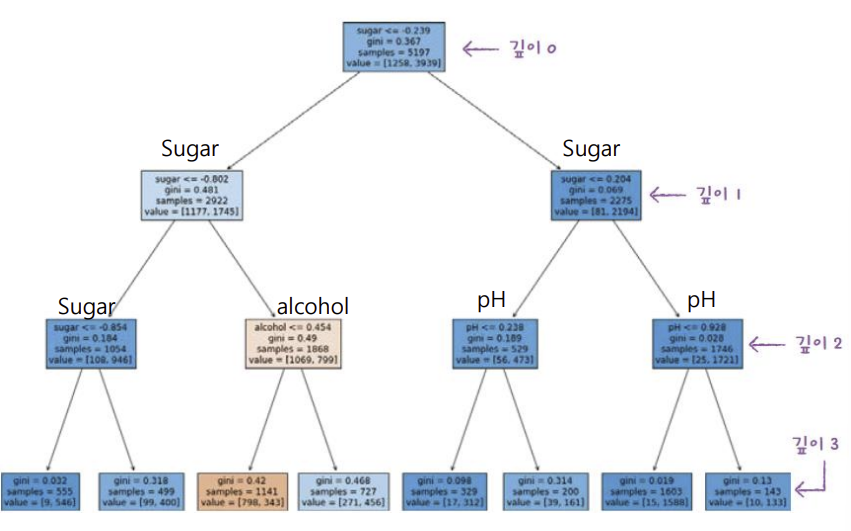

- 앞서 불순도를 기준으로 샘플을 나누고 불순도는 클래스별 비율을 가지고 계산했다.

- 샘플을 어떤 클래스 비율로 나누는지 계산할 때 특성값의 스케일이 영향을 미치지 않는다.

- 따라서 결정 트리는 표준화 전처리 과정이 필요가 없다.

- 전처리 하기 전 훈련 세트, 테스트 세트로 결정 트리 모델을 다시 학습하겠다.

dt = DecisionTreeClassifier(max_depth=3, random_state=42)
dt.fit(train_input, train_target)
print(dt.score(train_input, train_target))
print(dt.score(test_input, test_target))
>>> 0.8454877814123533
>>> 0.8415384615384616

 

- 마지막으로 결정 트리는 어떤 특성이 가장 유용한지 나타내는 특성 중요도를 계산해준다.

- 이 트리의 루트 노드와 깊이 1에서 당도를 사용했기 때문에 아마도 당도(sugar)가 가장 유용한 특성일 것이다.

print(dt.feature_importances)
>>> [0.12345626 0.86862934 0.0079144 ]

 

- 두 번째 특성인 당도가 0.87 정도로 특성 중요도가 가장 높다.

- 세가지 값을 다 더하면 1이 된다.

- 특성 중요도는 각 노드의 정보 이득과 전체 샘플에 대한 비율을 곱한 후 특성별로 더해서 계산한다.

 

- 사이킷런의 결정 트리 클래스가 제공하는 매개변수 중 min_impurity_decrease 설정은 불필요한 분할을 줄이고 과적합을 방지한다.

dt = DecisionTreeClassifier(min_impurity_decrease = 0.0005, random_state=42)
dt.fit(train_input, train_target)
print(dt.score(train_input, train_target))
print(dt.score(test_input, test_target))
>>> 0.8874350586877044
>>> 0.8615384615384616

plt.figure(figsize=(20,15))
plot_tree(dt, filled=True, feature_names=['alcohol','sugar','pH'])
plt.show()

 

2. 교차 검증과 그리드 서치

검증세트

- 테스트 세트를 사용하지 않고 모델이 과대적합인지 과소적합인지 판단하는 방법은 훈련 세트를 또 나누는 방법이 있다.

- 이 데이터를 검증 세트(validation set)라고 부른다.

import pandas as pd
wine = pd.read_csv('https://bit.ly/wine_csv_data')

data = wine[['alcohol','sugar','pH']]
target = wine['class'].to_numpy()

from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(data, target, test_size=0.2, random_state=42)

 

- 그 다음 train_input과 train_target을 다시 train_test_split() 함수에 넣어서 검증 세트를 만든다.

sub_input, val_input, sub_target, val_target = train_test_split(train_input, train_target, test_size=0.2, random_state=42)
print(sub_input.shape, val_input.shape)
>>> (4157, 3) (1040, 3)

 

- 검증 세트를 만들면 훈련 세트가 줄어든다.

- 보통 많은 데이터를 훈련에 사용할 수록 좋은 모델이 만들어진다.

- 이럴 때 교차 검증을 이용하면 안정적인 검증 점수를 얻고 훈련에 더 많은 데이터를 사용할 수 있다.

 

- 위 그림처럼 훈련세트를 세 부분으로 나눠서 교차 검증을 수행하는 것을 3-폴드 교차 검증이라고 한다.

- 통칭 k-폴드 교차 검증 (k-fold cross validation)이라고 한다.

from sklearn.model_selection import cross_validate
scores = cross_validate(dt, train_input, train_target)
>>> {'fit_time': array([0.00556493, 0.00580692, 0.00420165, 0.00367594, 0.00443721]),
     'score_time': array([0.001544  , 0.00204611, 0.00113249, 0.00140691, 0.00113153]), 
     'test_score': array([0.84230769, 0.83365385, 0.84504331, 0.8373436 , 0.8479307 ])}
     
import numpy as np
print(np.mean(scores['test_score']))
>>> 0.8412558303102096

 

- 한 가지 주의할 점은 cross_validate()는 훈련 세트를 섞어 폴드를 나누지 않는다.

- 교차 검증을 할 때 훈련 세트를 섞으려면 분할기(splitter)를 지정해야 한다.

 

- cross_validate() 함수는 기본적으로 회귀 모델일 경우 KFold 분할기를 사용하고,

- 분류 모델일 경우 타깃 클래스를 골고루 나누기 위해 StratifiedKFold를 사용한다.

from sklearn.model_selection import StratifiedKFold
scores = cross_validate(dt, train_input, train_target, cv = StratifiedKFold())
print(np.mean(scores['test_score']))
>>> 0.8412558303102096

# 10-fold cross validation
splitter = StratifiedKFold(n_splits=10, shuffle=True, random_state=42)
scores = cross_validate(dt, train_input, train_target, cv=splitter)
print(np.mean(scores['test_score']))
>>> 0.8335549132947977

 

하이퍼파라미터 튜닝

- 머신러닝 모델이 학습하는 파라미터를 모델 파라미터라고 한다.

- 반면에 모델이 학습할 수 없어서 사용자가 지정해야만 하는 파라미터를 하이퍼파라미터라고 한다.

- 먼저 라이브러리가 제공하는 기본값을 그대로 사용해 모델을 훈련하고

- 검증 세트의 점수나 교차 검증을 통해 매개변수를 조금씩 바꿔가면서 모델을 훈련한다.

 

- 이런 매개변수를 수동 조정 하는 것은 매개변수가 많아지면 문제가 복잡해지고 재현성이 낮아진다.

- 그리드 서치(Grid Search) 방법은 하이퍼파라미터 탐색과 교차 검증을 한 번에 수행한다.

from sklearn.model_selection import GridSearchCV
params = {'min_impurity_decrease' : [0.0001, 0.0002, 0.0003, 0.0004, 0.0005]}

gs = GridSearchCV(DecisiomTreeClassifier(random_state=42), params, n_jobs=-1)
gs.fit(train_input, train_target)

dt = gs.best_estimator_
print(dt.score(train_input, train_target))
>>> 0.9615162593804117

print(gs.best_params)
>>> {'min_impurity_decrease': 0.0001}

print(gs.cv_results_['mean_test_score'])
>>> [0.86819297 0.86453617 0.86492226 0.86780891 0.86761605]

best_index = np.argmax(gs.cv_results_['meam_test_score'])
print(gs.cv_results_['params'][best_index])
>>> {'min_impurity_decrease': 0.0001}

 

params = {'min_impurity_decrease' : np.arange(0.0001, 0.001, 0.0001),
          'max_depth' : range(5,20,1),
          'min_samples_split' : range(2,100,10)}
          
gs = GridSearchCV(DecisionTreeClassifier(random_state=42), params, n_jobs=-1)
gs.fit(train_input, train_target)

print(gs.best_params)
>>> {'max_depth': 14, 'min_impurity_decrease': np.float64(0.0004), 'min_samples_split': 12}

print(np.max(gs.cv_results_['mean_test_score']))
>>> 0.8683865773302731

 

랜덤 서치

- 매개변수의 값이 수치일 때 값의 범위나 간격을 미리 정하기 어렵기 때문에 랜덤 서치(Random Search)를 사용하면 좋다.

- 랜덤 서치에는 매개변수 값의 목록을 전달하는 것이 아니라 매개변수를 샘플링 할 수 있는 확률 분포 객체를 전달한다.

from scipy.stats import uniform, randint

rgen = randint(0,10)
rgen.rvs(10)
>>> [0 4 5 0 2 6 1 6 2 0]

ugen = uniform(0,1)
ugen.rvs(10)
>>> [0.81361577 0.15506291 0.07832085 0.99309424 0.76224274 0.7738125 
     0.69291207 0.53793199 0.55789721 0.48067332]

np.unique(rgen.rvs(1000), return_counts=True)
>>> (array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),
     array([ 97,  91, 101, 106,  95,  95,  92, 100, 101, 122]))

 

- 랜덤 서치에 randint와 uniform 클래스 객체를 넘겨주고 몇 번 샘플링 해서 최적의 매개변수를 찾으라고 명령할 수 있다.

- 탐색할 매개변수의 딕셔너리에는 min_samples_leaf 매개변수를 추가한다.

- 이 매개변수는 리프 노드가 되기 위한 최소 샘플의 개수이다.

params = {'min_inpurity_decease' : uniform(0.0001, 0.001),
          'max_depth' : randint(20,50),
          'min_samples_split' : randint(2,25),
          'min_samples_leaf' : randint(1,25)}
          
from sklearn.model_selection import RandomizedSearchCV
gs = RandomizedSearchCV(DecisionTreeClassifier(random_state=42), params, n_iter=100, n_jobs=-1, random_state=42)
gs.fit(train_input, train_target)

print(gs.best_params_)
>>> {'max_depth': 39, 'min_impurity_decrease': np.float64(0.00034102546602601173), 'min_samples_leaf': 7, 'min_samples_split': 13}

print(np.max(gs.cv_results_['mean_test_score']))
>>> 0.8695428296438884

dt = gs.best_estimator_
print(dt.score(test_input, test_target))
>>> 0.86

 

3. 트리의 앙상블

랜덤 포레스트

- 랜덤 포레스트는 결정 트리는 랜덤하게 만들어 결정 트리의 숲을 만든다.

- 그리고 각 결정 트리를 학습하고 평균 예측 또는 다수결로 최종 예측을 만든다.

 

- 먼저 랜덤 포레스트는 각 트리를 훈련하기 위한 데이터를 랜덤하게 만든다.

- 우리가 입력한 훈련 데이터에서 랜덤하게 샘플을 추출하여 훈련 데이터를 만든다. -> 배깅

- 부트스트랩 샘플이란 주어진 데이터셋에서 중복을 허용하여 무작위로 샘플을 추출하는 방법이다.

- 기본적으로 부트스트랩 샘플은 훈련 세트의 크기와 같게 만든다.

 

- 각 노드를 분할할 때 전체 특성 중에서 일부 특성을 무작위로 고른다.

- RandomForestClassifier는 기본적으로 전체 특성 개수의 제곱근만큼의 특성을 선택한다.

- RandomForestRegressor는 전체 특성을 사용한다.

 

- 랜덤 포레스트는 랜덤하게 선택한 샘플과 특성을 사용하기 때문에 과적합 방지에 강하고 병렬 처리에 용이하다.

 

rf = RandomForestClassifier(n_jobs=-1, random_state=42)
scores = cross_validate(rf, train_input, train_target, return_train_score=True, n_jobs=-1)
print(np.mean(scores['train_score']), np.mean(scores['test_score']))
>>> 9973541965122431 0.8905151032797809

rf.fit(train_input, train_target)
print(rf.feature_importances_)
>>> [0.23167441 0.50039841 0.26792718]

 

- RandomForestClassifier에는 자체적으로 모델을 평가하는 점수를 얻을 수 있다.

- 부스트랩 샘플을 만들 때 부스트랩 샘플에 포함되지 않고 남는 샘플이 있다.

- 이러한 샘플을 OOB(out of bag) 샘플이라고 한다.

- 이 남은 샘플을 사용해 부스트랩 샘플로 훈련한 결정 트리를 평가할 수 있다. -> 검증 세트

rf = RandomForestClassifier(oob_score=True, n_jobs=-1, random_state=42)
rf.fit(train_input, train_target)
print(rf.oob_score_)
>>> 0.8934000384837406

 

엑스트라 트리

- 엑스트라 트리(Extra Tree)는 랜덤 포레스트와 비슷하게 동작한다.

- 엑스트라 트리는 부스트랩 샘플을 사용하지 않는다는 점이 있다.

- 즉 결정트리를 만들 때 전체 훈련 세트를 사용한다.

- 대신 노드를 분할할 때 가장 좋은 분할을 찾는 것이 아니라 무작위로 분할한다.

- 결정 트리에서 특성을 무작위로 분할하면 성능은 낮아지지만 많은 트리를 앙상블 하기 때문에 과대적합을 막고 검증 세트의 점수를 높일 수 있다.

from sklearn.ensemble import ExtraTreesClassifier
et = ExtraTreesClassifier(n_jobs=-1, random_state=42)
scores = cross_validate(et, train_input, train_target, return_train_score=True, n_jobs=-1)
print(np.mean(scores['train_score']), np.mean(scores['test_score']))
>>> 0.9974503966084433 0.8887848893166506

 

- 보통 엑스트라 트리가 무작위성이 더 크기 때문에 랜덤 포레스트보다 더 많은 결정 트리를 훈련해야 한다.

- 하지만 랜덤하게 노드를 분할하기 때문에 빠른 계산 속도가 엑스트라 트리의 장점이다.

 

그레디언트 부스팅

- 그레디언트 부스팅(gradient boosting)은 깊이가 얕은 결정 트리를 사용하여 이전 트리의 오차를 보완하는 방식으로 앙상블 하는 방법이다.

- 각 트리는 잔차를 줄이는 방향으로 학습하고 경사하강법을 사용해 트리를 앙상블에 추가한다.

- 높은 정확도도 가능하지만 계산량이 많고 병렬화가 어렵다.

- 분류에서는 로지스틱 손실 함수를 사용하고 회귀에서는 평균 제곱 오차 함수를 사용한다.

from sklearn.esemble import GradientBoostingClassifier
gb = GradientBoostingClassifier(random_state=42)
scores = cross_validate(gb, train_input, train_target, return_train_score=Ture, n_jobs=-1)
print(np.mean(scores['train_score']), np.mean(scores['test_score']))
>>> 0.8881086892152563 0.8720430147331015

gb = GradientBoostingClassifier(n_estimators=500, random_state=42)
scores = cross_validate(gb, train_input, train_target, return_train_score=Ture, n_jobs=-1)
print(np.mean(scores['train_score']), np.mean(scores['test_score']))
>>> 0.9215896435285418 0.8749283704745687

gb.fit(train_input, train_target)
print(gb.features_importances_)
>>> [0.14231164 0.70598825 0.1517001 ]

 

히스토그램 기반 그레디언트 부스팅

- 그레디언트 부스팅의 개선 버전으로, 생성 값을 구간으로 분할하여 학습 속도와 메모리 사용량을 개선한다.

from sklearn.ensemble import HistGradientBoostingClassifier

hgb = HistGradientBoostingClassifier(random_state=42)
scores = cross_validate(hgb, train_input, train_target, return_train_score=True, n_jobs=-1)

print(np.mean(scores['train_score']), np.mean(scores['test_score']))
>>> 0.9321723946453317 0.8801241948619236

from sklearn.inspection import permutation_importance

hgb.fit(train_input, train_target)
result = permutation_importance(hgb, train_input, train_target, n_repeats=10,
                                random_state=42, n_jobs=-1)
print(result.importances_mean)
>>> [0.08876275 0.23438522 0.08027708]

result = permutation_importances(hgb, test_input, test_target, n_repeats=10, random_state=42, n_jobs=-1)
print(result.importances_mean)
>>> [0.05969231 0.20238462 0.049     ]

hgb.score(test_input, test_target)
>>> 0.8723076923076923