훈련 세트와 테스트 세트
지도 학습과 비지도 학습
머신러닝 알고리즘은 크게 지도 학습과 비지도 학습으로 나뉜다.
지도 학습 알고리즘은 훈련하기 위한 데이터와 정답이 필요하다.
지도 학습에서는 데이터와 정답을 input과 target 이라고 하고 이 둘을 합쳐 training data라고 부른다.
앞 chapter에서 언급했듯이 입력으로 사용된 길이와 무게를 feature 라고 한다.
훈련 세트와 테스트 세트
머신러닝 알고리즘의 성능을 제대로 평가하려면 훈련 데이터와 평가에 사용할 데이터가 각각 달라져야 한다.
이렇게 하는 가장 간단한 방법은 평가를 위해 또 다른 데이터를 준비하거나 이미 준비된 데이터 중에서 일부를 떼어 내어 활용한다.
평가에 사용하는 데이터를 test set, 훈련에 사용하는 데이터를 train set이라고 부른다.
train_input = fish_data[:35]
trian_target = fish_target[:35]
test_input = fish_data[35:]
test_target = fish_target[35:]
슬라이싱 연산으로 처음 35개 샘플을 훈련 세트로 선택했고 나머지 14개의 샘플을 테스트 세트로 선택했다.
kn.fit(train_input, train_target)
kn.score(test_input, test_target)
>>> 0.0
샘플링 편향
정확도가 0이 나왔다.
훈련하는 데이터와 테스트하는 데이터에는 도미와 빙어가 골고루 섞여야 한다.
위와 같이 데이터를 나누면 train set에는 도미만 있기 때문에 test set가 무엇이든 도미라고 예측해버린다.
이렇게 train set와 test set가 골고루 섞여있지 않은 걸 sampling bias 라고 한다.
input_arr = np.array(fish_data)
target_arr = np.array(fish_target)
생선 데이터를 넘파이 배열로 준비하고 이 배열에서 랜덤하게 샘플을 선택해서 train set와 test set를 만들 것이다.
여기서 주의할 점은 input_arr와 target_arr에서 같은 위치는 함께 선택되어야 한다.
np.random.seed(42)
index = np.arange(49)
np.random.shuffle(index)
print(index)
>>> [13 45 47 44 17 27 26 25 31 19 12 4 34 8 3 6 40 41 46 15 9 16 24 33
30 0 43 32 5 29 11 36 1 21 2 37 35 23 39 10 22 18 48 20 7 42 14 28
38]
arange() 함수를 사용해서 인덱스를 만들고 이 인덱스를 랜덤하게 섞는다.
train_input = input_arr[index[:35]]
train_target = target_arr[index[:35]]
test_input = input_arr[index[35:]]
test_target = target_arr[index[35:]]
이렇게 해서 모든 데이터 준비가 끝났다. 잘 섞였는지 산점도를 그려보겠다.
import matplotlib.pyplot as plt
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(test_input[:,0], test_input[:,1])
plt.xlabel('length')
plt.ylabel('weight')
두 번째 머신러닝 프로그램
kn.fit(train_input, train_target)
kn.score(test_input, test_target)
>>> 1.0
kn.predict(test_input)
>>> array([0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0])
test_target
>>> array([0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0])
테스트 세트에 대한 예측 결과가 정답과 일치한다.
데이터 전처리
전에는 파이썬 리스트를 순회하면서 원소를 하나씩 꺼내 2차원 리스트로 직접 구성했다.
이제 column_stack() 함수를 사용해서 2차원 리스트로 구성해보자.
import numpy as np
fish_data = np.column_stack((fish_length, fish_weight))
동일한 방법으로 target 데이터도 만들어보자.
np.ones()와 np.zeros() 배열을 만들고 두 배열을 연결하는 np.concatnate() 함수를 사용한다.
fish_target = np.concatnate((np.ones(35), np.zeros(14)))
print(fish_target)
>>> [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0.]
사이킷런으로 훈련 세트와 테스트 세트 나누기
우리는 사이킷런의 train_test_split() 함수를 사용해서 train set와 test set로 나누어줄 것이다.
from sklearn.model_selection import train_test_split
train_input, train_target, test_input, test_target = train_test_split(fish_data, fish_target, random_state=42)
앞에서 무작위로 섞기 전에 np.random.seed() 함수를 사용했는데 train_test_split() 함수에는 자체적으로 랜덤 시드를 지정할 수 있는 random_state 매개변수가 있다.
이 함수는 기본적으로 25%의 테스트 세트를 떼어낸다.
도미와 빙어가 잘 섞였는지 테스트 데이터를 출력해보자.
print(test_target)
>>> [1. 0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
원래 도미와 빙어의 비율은 2.5:1이지만 테스트 세트의 비율은 3.3:1이다.
이전 절에서 본 샘플링 편향이 일어난 것이다.
이 문제를 해결하기 위해 train_test_split() 함수의 stratify 매개변수를 사용해서 클래스 비율에 맞게 데이터를 나눈다.
train_input, train_target, test_input, test_target = train_test_split(fish_data, fish_target, stratify=fish_target, random_state=42)
print(test_target)
>>> [0. 0. 1. 0. 1. 0. 1. 1. 1. 1. 1. 1. 1.]
수상한 도미 한 마리
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier()
kn.fit(train_input, train_target)
kn.score(test_input, test_target)
print(kn.predict([[25,150]]))
>>> [0.]plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25,150,marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
indexes 베열을 사용해 훈련 데이터 중에서 이웃 샘플을 따로 구분해서 그려보겠다.
distances, indexes = kn.kneighbors([[25,150]])
print(distances, indexes)
>>> [[ 92.00086956 130.48375378 130.73859415 138.32150953 138.39320793]] [[21 33 19 30 1]]
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25,150,marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1],marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
예측 결과와 마찬가지로 가장 가까운 이웃에 도미가 하나 밖에 없다.
산점도를 보면 직관적으로 도미와 가깝게 보이는데 왜 가장 가까운 이웃을 빙어라고 생각한 걸까?
산점도를 다시 보면 삼각형 샘플에 가장 가까운 첫 번째 샘플까지의 거리는 92이고, 그 외 가장 가까운 샘플들은 130,138이다.
하지만 그래프에 나타난 거리 비율이 조금 이상하다.
x축의 범위를 0~1000으로 맞춰보겠다.
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25,150,marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1],marker='D')
plt.xlim((0,1000))
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
x축과 y축의 범위를 동일하게 맞추니 모든 데이터가 수직으로 늘어선 형태가 되었다.
이런 데이터라면 생선의 길이는 가까운 이웃을 찾는데 영향을 못 미친다. 오로지 생선의 무게만 고려 대상이 된다.
두 특성의 값이 놓인 범위가 다른 것이다. 이를 두 특성의 스케일이 다르다고 말한다.
이 K-Nearest Neighbors 알고리즘은 샘플 간의 거리에 영향을 많이 받으므로 제대로 사용하려면 특성값을 일정한 기준으로 맞춰야 한다.
이러한 작업을 데이터 전처리라고 부른다.
가장 많이 사용하는 전처리 방법은 표준점수이다.
표준점수는 각 특성 값이 평균에서 표준편차의 몇 배 만큼 떨어져 있는지 나타내기 때문에 실제 특성값 크기와 상관 없이 동일한 조건으로 비교할 수 있다.
mean = np.mean(train_input, axis=0)
std = np.std(train_input, axis=0)
train_scaled = (train_input - mean) /std
특성마다 값의 스케일이 다르기 때문에 평균과 표준편차는 각 특성 별로 계산해야 한다.
전처리 데이터로 모델 훈련하기
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(25,150,marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
훈련 세트를 평균으로 빼고 표준편차로 나누었기 때문에 값의 범위가 많이 달라졌다.
샘플을 동일한 비율로 변환하지 않으면 이런 현상이 발생할 것이다.
여기서 중요한 점은 훈련세트의 mean, std를 이용해서 변환해야 한다.
new = ([25,150]-mean) / std
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(25,150,marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
앞에서 그린 산점도와 거의 동일하다.
크게 달라진 점은 x축과 y축 범위가 -1.5~1.5로 바뀌었다는 것이다.
kn.fit(train_scaled, train_target)
test_scaled = (test_input - mean) / std
kn.score(test_sclaed, test_target)
print(kn.predict([new]))
>>> [1.]
test set의 스케일도 반드시 train set의 평균과 표준편차로 스케일을 조정해야 한다.
distances, indexes = kn.kneighbors([new])
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.scatter(train_scaled[indexes,0],train_scaled[indexes,1],marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()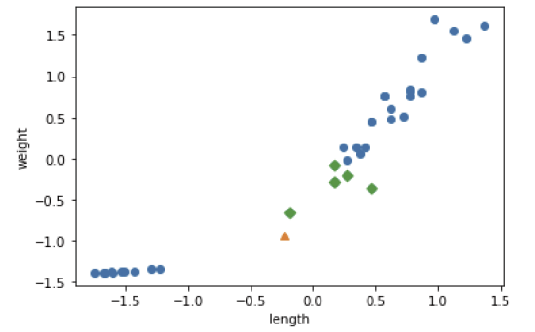
'Major Study > 25-1 Machine Learning' 카테고리의 다른 글
| [Machine Learning] chapter5 - 트리 알고리즘 (0) | 2025.05.14 |
|---|---|
| [Machine Learning] chapter4 - 로지스틱 회귀 (0) | 2025.04.30 |
| [Machine Learning] chapter3 - 회귀 알고리즘과 모델 규제 (0) | 2025.04.11 |
| [Machine Learning] chapter 1 - 머신러닝 (0) | 2025.04.01 |



