01 확률의 정의
확률 개요
- 고전적 확률 : 수학적 확률, 통계적 확률, 기하적 확률, 주관적 확률
- 확률은 불확실성 사건의 발생 측도이다.
- 경험적 확률에서는 비율을 확률로 간주한다.
- 공리적 확률에 의하여 사건을 집합으로 간주하여 확률 측도로 일반화
확률 시행
- 시행이란 어떤 행위를 지칭하는 것이다.
- 시행의 결과는 불확실성으로 인해 확정할 수 없으나 예상할 수 있어야 한다.
ex) 확률시행 : 동전 하나를 던진다.
결과의 예상 : 앞면 아니면 뒷면
- 결과를 확정할 수 있는 시행은 확률시행이 아니다. ex) 해가 뜨는 방향
확률 실험
- 단일 확률시행 또는 복합 확률시행을 통칭
- 단일 확률 시행 ex) 주사위 하나를 던진다. / 동전 두 개를 동시에 한 번 던진다.
- 복합 확률 시행 ex) 동전 하나를 세 번 던진다. / 동전 두 개를 동시에 두 번 던진다.
표본공간
- 어떤 확률 실험에서 발생가능한 결과물을 모두 모아 놓은 집합
ex) 동전 하나를 던지는 확률 실험의 표본 공간 (S) = {앞면,뒷면}
동전 하나를 두 번 던지는 확률 실험의 표본 공간 (S) = {(앞면,앞면, (앞면, 뒷면), (뒷면,앞면), {뒷면,뒷면)}
- 표본공간의 표현은 다양하다. 사건의 표현도 다양하다.
- 그렇기 때문에 계량화가 필요하다 (확률변수)
사건
- 표본공간의 부분집합
- 공사건, 근원사건, 전사건
ex) 동전 하나를 던지는 확률실험
- 사건 : {}=공사건, {H}, {T}=근원사건, {H,T}=전사건
- 합사건 : A∪B -> 논리합에 기반한 사건
- 곱사건 : A ∩ B -> 논리곱에 기반한 사건
- 여사건 : A^c -> 사건 A와 상호 배타적 관계를 나타내는 사건
수학적 확률
- 표본공간에서 해당사건이 차지하는 비의 합
- 모든 근원사건들의 발생 가능성이 동등할 때만 사용
ex) 동전 하나를 던지는 확률시행에서 앞면이 나오는 확률 = 뒷면이 나오는 확률
통계적 확률
- n번의 시행에서 해당 사건이 r회 발생하였을 때 그 상대돗수의 극한


기하적 확률
- 표본공간이 어떤 영역으로 나타날 때의 확률

주관적 확률
- 자신의 지식이나 경험에 의하여 주관적으로 어떤 사건의 발생가능성에 대해 부여한 값
ex) A와 B팀의 10번의 경기에서 60% 이겼다면 이번 경기에도 A팀이 우승할 확률은 7/11
공리적 확률
- 집합 이론과 측도론을 기반으로 체계화
- <전체적 선언> : 1. 표본공간은 하나의 사건이다.
2. 한 사건의 여집합도 사건이다.
3. 사건들의 무한 합 연산 결과도 하나의 사건이다.
- <확률의 공리> 조건을 만족하는 P를 공리적 확률이라 한다.
1. 표본공간 S에 대하여 P(S)=1이다.
2. 사건 A에 대하여 P(A)>=0이다.
3. 배반사건 A1,A2,...에 대하여 밑에 식을 만족한다.

확률의 기본 성질

조건부 확률
- 두 사건 A,B에 대하여 P(B)>0일 때 P(A ∩B)/P(B)를 사건 B가 발생했을 때, 사건 A의 조건부 확률이라 한다.
- 사건 B를 새로운 표본공간으로 간주할 때의 사건 A ∩B의 발생확률을 의미한다.

사건의 독립
- P(B)>0에 대하여 P(A|B) = P(A|B^c)일 때 A,B는 서로 독립이라 한다.
- 사건 A의 발생 확률이 사건 B의 발생 여부에 따라 변하지 않음을 의미한다.
- 동치조건 P(A ∩B) = P(A)P(B)을 독립의 정의조건으로 사용할 수 있다.
표본공간의 분할
- 표본공간 S의 사건 E1,E2,...En에 대해

일 때, E1,E2,...En을 S의 분할이라 한다.
전 확률의 법칙
- 사건 E1,E2,...En이 S의 분할일 때 A⊂S에 대해

- 위 확률 P(A)를 사건 A의 전 확률 (total probability)라 한다.

베이즈 공식
- 사건 B1,B2,...,Bn이 S의 분할일 때 A⊂S에 대하여

- 이를 베이즈 공식이라 한다.

02 확률변수와 확률분포
이산형 확률변수
- 표본공간 S가 이산형 집합일 때 정의한다.
- 표본공간에서 정의된 실가함수를 확률변수라 한다.

ex) 동전 하나를 던지는 확률실험에서 확률변수 X의 정의
{앞면} = { s∈S | X(s)=1 }
{뒷면} = { s∈S | X(s)=0 }
위의 사건들을 각각 X=1, X=0으로 간단히 표현한다.

-> 무작위로 한 가구를 뽑았을 때 그 가구의 자녀 수를 X라 하면, X=2는 자녀수가 2인 가구인 뽑혔음을 의미한다.
-> 상대도수는 뽑힌 가구가 해당 범주에 속할 확률로 간주한다. P(X=2) = 0.25
확률질량함수
- 표본공간 S 위에서 정의된 이산형 확률변수 X에 대하여 함수 P(X=x)를 X의 확률질량함수라고 한다.
- 확률질량함수의 고유한 성질 세 가지

- Sx는 X의 치역으로 X의 공간이라고 한다.
이산형 확률변수의 평균, 분산, 표준편차
- 이산형 확률변수 X의 확률질량함수가 P(X=x), x ∈ Sx일 때,
- 평균(기댓값) :

- 분산 :

- 분산의 양의 제곱근은 표준편차라고 한다.
기댓값의 성질
- 상수의 기댓값은 자기자신이다. (E(k) = k)
- 합의 기호 ∑ 의 성질에 의하여 합, 차, 상수배는 보존된다. ( E(aX+Y) = aE(X) + bE(Y) )
분산의 성질
- 모든 편차의 제곱들의 평균으로 항상 0보다 크거나 같다.
- 제곱의 평균과 평균의 제곱 간의 차와 같다. ( E(X- μ)^2 = E(X^2) - μ^2 )
- Var(a) = 0
- Var(aX) = a^2Var(X)
- Var(aX+b) = a^2Var(X) + 0
표준편차에 의한 데이터의 비중
- 체비셰프 부등식 : P(|X- μ| <= kσ) >= 1-1/k^2 (k>1)
-> 평균으로부터 k배의 표준편차 이내에 있는 데이터점들의 최소 비중이 (1-1/k^2) x 100%임을 의미한다.
ex) k=2 : 1-1/4=3/4이므로 2표준편차 이내의 데이터 비중은 최소 75%이다.
연속형 확률변수와 확률밀도함수
- 어떤 확률변수 X가 다음의 성질을 만족할 때, 함수 f(x)를 X의 확률밀도함수라고 한다.
- 다음 성질을 갖는 확률변수를 연속형 확률변수라고 한다.

연속형 확률변수의 평균, 분산, 표준편차
- 연속형 확률변수 X의 확률밀도함수가 f(x), x ∈ Sx일 때,
- 평균 :

- 분산 :

- 분산의 양의 제곱근을 표준편차라 한다.
연속형 확률변수에 관한 확률의 성질
- P(X=a) = 0
- P(a < X < b) = P(a <= X < b) = P(a < X <= b) = P(a <= X <= b)
* a,b ∈ Sx
03 확률분포 종류
정규분포

- 확률변수 X의 확률밀도함수가 다음과 같을 때, X는 평균이 μ이고, 분산이 σ^2 인 정규분포를 따른다.
- X ~ N( μ, σ^2)
정규분포의 확률밀도함수의 곡선

- μ는 위치 모수 (location parameter), σ는 척도 모수 (규모 모수, scale parameter)
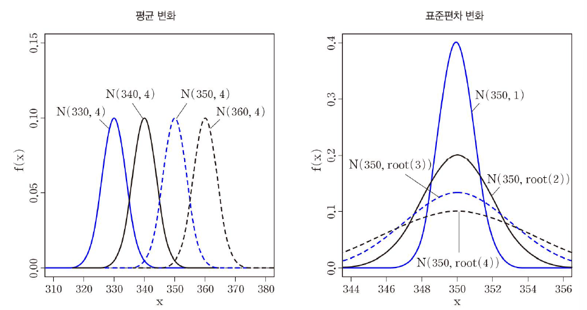
- σ에 따른 데이터 비중


표준정규분포
- 평균이 0이고 분산이 1인 정규분포이다.
- 표준정규분포의 확률변수는 Z로 나타낸다. -> Z~N(0,1)

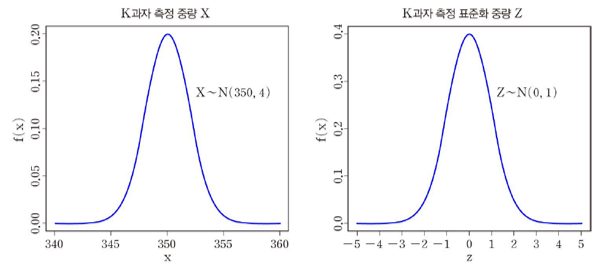
표준화
- X~N(μ, σ^2) 을 Z~N(0,1)로 변환하는 것이다.
- X~N(μ, σ^2)일 때, Z = (X- μ)/ σ ~ N(0,1)
- 다른 정규분포를 따르는 두 데이터 점의 위치적 비교나 정규분포 관련 확률의 계산에 쓰인다.

'Major Study > 25-1 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 5장. 추정 (0) | 2025.05.27 |
|---|---|
| [확률과 통계] 4장. 모집단과 표본 (0) | 2025.04.15 |
| [확률과 통계] 3장. 확률과 확률변수 2 (0) | 2025.04.06 |
| [확률과 통계] 2장. 정형자료 분포지표와 시각화 (0) | 2025.04.01 |
| [확률과 통계] 1장. 통계학과 빅데이터 (1) | 2025.03.30 |



