01 모집단과 표본
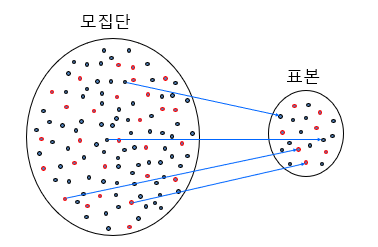
모집단 (population)
- 연구나 조사의 관심 대상 전체의 모임이다.
- 때로는 관심대상 전체 측정값들의 집합을 모집단으로 간주한다.
표본 (sample)
- 모집단의 부분집합
- 모집단을 잘 설명하기 위해서는 대표성을 갖춰야 한다.
전수조사
- 모집단 전체를 조사하는 것이다.
표본조사
- 추출된 표본에 의하여 조사하는 것이다.
- 모집단의 특성을 추정을 할 때 사용한다.
- 표본추출에서 선택편향이 발생하면 알맞은 조사방법이라고 볼 수 없다.
통계량
- 모수의 추정을 위해 사용되는 표본들의 함수이다. (추정량)

통계치
- 통계량의 값이다. (추정치)

모집단의 분포 ex) 베르누이 분포 X ~ Bernoulli(p)
이항분포 X ~ B(n,p)
포아송 분포 X ~ Poisson(λ)
정규분포 X ~ N(μ,σ^2)
02 표본추출 (sampling)
반복 가능 여부에 따른 표본 추출 방법
- 복원추출 (sampling with replacement)
- 비복원추출 (sampling with replacement)
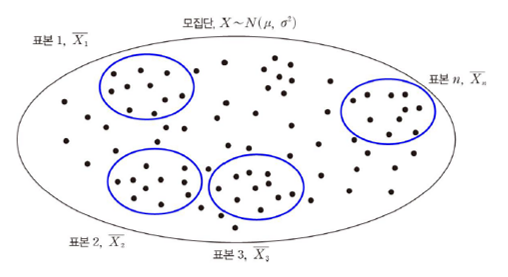
단순확률추출법 (simple random sampling)
- 무작위적(random), 독립적(independent) 추출
- 모집단의 특성을 잘 대표하는 표본 -> 확률표본이라 한다.
- 표본의 분포가 모집단의 분포와 동일하다는 주장이 있어야 한다.
ex) X1, X2, ... , Xn은 정규분포 N(μ, σ^2)를 따르는 모집단에 추출된 확률 표본 <-> X1,X2,...,Xn ~ i.i.d N(μ, σ^2)
표본평균과 표본분산
- 표본 X1, X2, ... , Xn 에 대하여

표본평균의 기댓값과 분산

03 중심극한 정리
정규분포를 따르는 모집단으로부터 추출된 표본평균의 분포 (표준화)
- X1,X2,..,Xn이 정규분포 N(μ, σ^2)를 따르는 모집단에 추출된 크기가 n인 확률표본일 때, 표본평균은 정규분포 N(μ, σ^2/n)를 따른다.


04 표본비율의 분포
모비율과 표본비율
- 모비율 p는 모집단에서 관심의 대상이 되는 특정한 성질을 갖는 개체들의 비율이다. ex) 성공률, 찬성률, 지지율
- 모비율 p의 추정량 p는 X = X1 + X2 + ... + Xn일 때 다음과 같다.

표본비율의 분포

05 오차의 개념
오차(error)의 유형
- 오차 = 참값 - 근사값
- 오차의 종류 : 1. 절대오차 = |참값-근사값|
2. 상대오차 = (참값-근사값)/참값
3. 상대절대오차 = |(참값-근사값)/참값|
오차에 의한 모수의 추정
- 참값의 추정값을 구하기 위해 사용된 근사값들이 x1,x2,...,xn일 때,
추정원리 1 : 절대 오차의 합을 최소화하는 값을 추정값으로 선택한다.

추정원리 2 : 오차의 제곱의 합을 최소화하는 값을 추정값으로 선택한다.
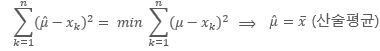
표본오차의 발생 원인
- 모집단 설정 이유, 선택 오류, 표집틀 오류, 무응답 오류
비표본오차
- 표본조사시 발생하는 오차 중 표본오차가 아닌 오차이다.
- 데이터의 정확도나 처리과정에서 발생한다.
- 표본편의에 의하여 발생하기 때문에 표본의 크기를 크게 해도 줄어들지 않는다.
'Major Study > 25-1 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 6장. 가설검정 (0) | 2025.05.29 |
|---|---|
| [확률과 통계] 5장. 추정 (0) | 2025.05.27 |
| [확률과 통계] 3장. 확률과 확률변수 2 (0) | 2025.04.06 |
| [확률과 통계] 3장. 확률과 변수 (0) | 2025.04.02 |
| [확률과 통계] 2장. 정형자료 분포지표와 시각화 (0) | 2025.04.01 |



