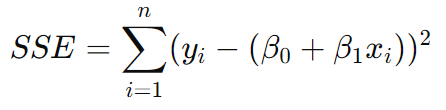01 단순선형회귀모형
추이파악과 예측모형

- 위 그래프는 광고비가 증가할수록 매출액이 증가하는 경향을 나타낸다.
- 위 그래프에서 모든 데이터점들을 지나는 최소 타원을 그리고 이 타원의 장축을 모형식으로 선택한다.
- 그 모형식은 두 변수 사이의 관계를 설명하기 위해 사용되는 막연한 관계 함수이며, 이를 추측함수라고 부른다.
- 데이터에 따라서 추측함수의 형태도 달라진다.
예측모형 (함수관계) 구축하기

- 왼쪽 그래프의 2번 모형은 주어진 데이터점들이 모두 식 위에 놓여있으므로 설명력이 100%이다.
- 2번 모형은 다른 표본을 적용하면 설명력이 달라질 수 있고, 표본이 크다면 식이 복잡하게 된다.
- 적은 표본으로 과도하게 높은 설명력을 갖도록 적합하는 것을 과대적합이라고 부른다.
02 최소제곱 추정량과 잔차제곱합
회귀모형의 구축
- 모집단의 두 변수 간 선형관계가 존재할지 여부를 판단한다. (표본에 의한다.)
- y = β0 + β1x
- β0와 β1을 절편 모수, 기울기라고 한다.
- i번째 데이터 점 (xi, yi)에 대해 εi = yi − (β0 + β1xi)는 오차이다.
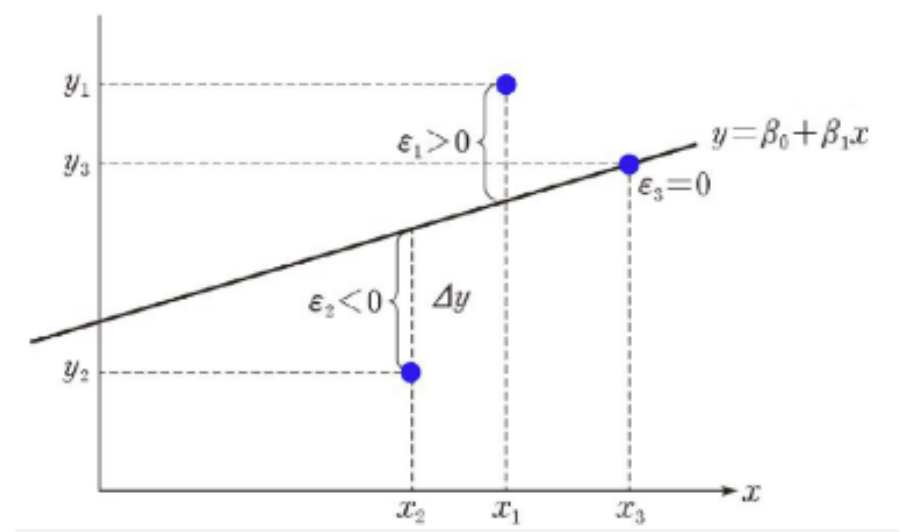
- 이때, 데이터점들의 x좌표와 y좌표 사이의 관계식은 y = β0 + β1x + ε이고, 이를 단순선형회귀모형이라고 한다.
회귀모형에서 오차항의 가정
1. 추측함수 위 아래로 데이터점들이 균일하다. -> 오차들의 평균 = 0, 동일분포
2. 오차항은 정규분포를 따른다.
3. 오차항은 서로 독립이다.
- 위 세가지를 종합하여 간단히 ε1, ε2, ... , εn ~ i.i.d N(0, σ^2)로 나타낸다.
모형의 적합
- 표본에 의하여 회귀 모수 β0, β1를 추정하는 행위이다.
- 원리는 최소제곱법을 이용한다.
- 최소제곱법이란 오차항의 제곱을 최소화하는 방법이다.
- 데이터가 (x1,y2), (x2,y2), ... ,(xn,yn)일 때 β0, β1은 다음을 만족한다.

- 회귀계수의 추정량 :

오차항의 분산 σ^2의 추정값 σ^2
- σ^2이 작을수록 두 변수간 상관관계는 높음을 의미한다.
- 추정량 σ^2의 값이 작을수록 데이터점은 회귀직선 가까이에 놓여있음을 의미한다.
- 잔차 : 적합후의 오차를 잔차(residual)이라고 하며, e1, e2, ... ,en로 나타낸다.
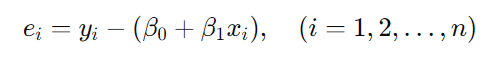
- 잔차제곱합 : 오차제곱합이라고 하며 SSE로 나타낸다.

- σ^2의 추정

03 회귀모형의 설명력
결정계수 R^2
- 제곱합의 분해 : SST = SSR + SSE
- 총 제곱합 - 회귀직선에 의한 제곱합 - 오차제곱합
- 결정계수

- 결정계수 식의 변형
: 여기서 r은 피어슨의 상관계수이다.
- -1 <= r <= 1

- 결정계수가 클수록 데이터점들이 회귀직선에 더 가까이 놓여있음을 의미하고,
- 이로 인해 결정계수를 회귀모형의 설명력이라 하기도 한다.
ex) R^2 = 0.9 -> 회귀모형의 설명력은 90%이다.
04 회귀계수의 추정과 검정
회귀계수 β1의 신뢰구간
- 관련 통계량과 분포

- β1에 대한 (1- α) 100% 신뢰구간

회귀계수 β1에 대한 가설검정 (양측검정)
step1. 가설설립 : H0: μ = 0 vs H1: μ != 0 / H0: μ = 0 vs H1: μ < 0 / H0: μ = 0 vs H1: μ > 0
-> 선형적 관련이 있다. -> 양의 상관관계가 있다. -> 양의 상관관계가 있다.
step2. 유의수준 : α step3. 검정통계량 선택 :
step4. 기각역 설정 :

step5. 의사결정 : 표본에 의하여 계산된 T의 값 t가 기각역에 속하면 H0 기각

-> 상관관계 X -> 양의 상관관계
'Major Study > 25-1 확률과 통계' 카테고리의 다른 글
| [확률과 통계] 7장. 두 모집단 비교와 두 변수 관계 (0) | 2025.05.29 |
|---|---|
| [확률과 통계] 6장. 가설검정 (0) | 2025.05.29 |
| [확률과 통계] 5장. 추정 (0) | 2025.05.27 |
| [확률과 통계] 4장. 모집단과 표본 (0) | 2025.04.15 |
| [확률과 통계] 3장. 확률과 확률변수 2 (0) | 2025.04.06 |